반응형
1. 동전 거스름돈
2. 이항계수
1. 동전 거스름돈
사용할 수 있는 동전의 종류 : 1원, 4원, 6원
이때, 거스름돈 8원에 대한 최소 동전 개수는 몇개인가?
- 그리디 - 6원, 1원, 1원
- 최적해 - 4원, 4원 => 완전 검색 방법 또는 동적계획법
1원을 선택하는 경우
- 1원 동전 한개 + 나머지 7원에 대한 최적해
4원을 선택하는 경우
- 4원 동전 한개 + 나머지 4원에 대한 최적해
6원을 선택하는 경우
- 6원 동전 한개 + 나머지 2원에 대한 최적해
위의 3가지 중에서 최적해를 선택한다
> 7원에 대한 최적해는 다시 1원, 4원, 6원 동전을 선택하고 나머지 액수에 대한 최적해이다.
재귀 알고리즘에 메모이제이션 적용
- change : 거스름돈 금액, coin = [6, 4, 1], 동전종류
- memo : 이미 구한 부분 문제의 해를 저장, -1로 초기화
def CoinChange(change):
if memo[change] != -1:
return memo[change]
else:
min = INF
for i in range(len(coin)):
if change - coin[i] >= 0:
ret = CoinChange(change - coin[i])
if min > ret : min = ret
memo[change] = min + 1
return memo[change]
동적계획법을 적용해서 상향식으로 구하기
f(n) = min{f(n-6), f(n-4), f(n-1)} + 1
def CoinChange_DP(change):
for N in range(1, change+1): # 거스름돈 금액을 1원부터 change원까지 늘려가면서 해를 구한다.
min = INF
for i in range(len(coin)): # 모든 동전 종류에 대해서 반복한다.
if N >= coin[i]: # 동전이 N보다 작은 금액인지 비교한다.
ret = memo[N - coin[i]] # 현재 금액에서 동전을 차감한 해가 최소값인지 비교
if min > ret : min = ret # 더 작을 경우 최소값 갱신
memo[N] = min + 1 # 최적해 저장
return memo[change]
2. 이항 계수 구하기

다음 식에서 ?에 들어갈 알맞은 값은 무엇인가?
이항정리
- 이항 다항식 x + y의 거듭제곱 (x + y)^n에 대해서, 전개한 각 항 x^k*y^(n-k)의 계수 값을 구하는 정리
- n개에서 k개의 조합의 가짓수인 nCk이고, 이를 이항 계수라고 한다.
이항 계수를 구하는 공식
1. factorial사용

2. 계산량이 많아 factorial을 사용하지않는 수식
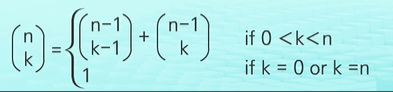
파스칼의 삼각형
이항 계수를 삼각형 모양의 기하학적 형태로 배열

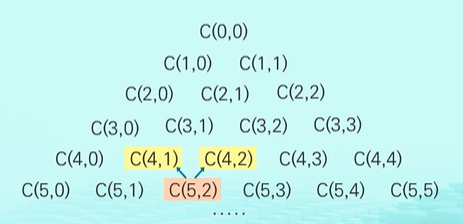
이것은 이항계수를 구하는 방법과 동일하다.
c(n, 0) = 1
c(n, n) = 1
c(n, k) = c(n-1, k-1) + c(n-1, k), n > k > 0
재귀 호출로 구현
def bino(n, k):
if k == 0 or k == n:
return 1
else:
return bino(n-1, k-1) + bino(n-1, k)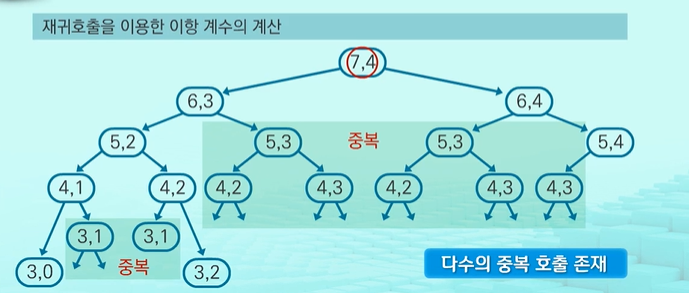
재귀호출은 많은 중복이 존재한다.
메모이제이션을 적용
def bino(n, k):
if k == 0 or k == n : return 1
if B[n][k] != -1:
return B[n][k]
else:
B[n][k] = bino(n-1, k-1) + bino(n-1, k)
return B[n][k]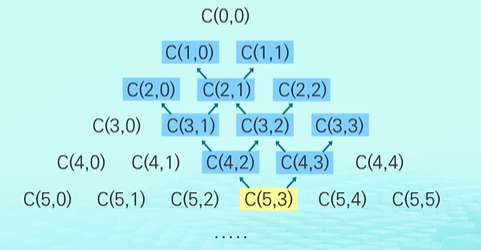
n = 5, k = 3인 경우를 구하기 위해서는 파란색으로 된 부분 문제를 구해야한다. 다음을 테이블로 표현해보자.

B[i][j]를 구하기 위해서는 B[i-1][j-1]과 B[i-1][j]가 이미 구해진 상태여야 한다. 동적계획법의 상향식 방식을 사용하기 위해서는 이러한 의존성에 위배되지 않아야한다.
동적계획법을 적용하여 이항계수 계산
리스트를 행 우선으로 탐색하는 것과 같은 순서로 계산하면 의존성에 위배되지 않는다.

B에 이미 구한 부분 문제의 해를 저장한다.
def bino(n, k):
for i in range(n+1): # 리스트에 행으로 사용할 i를 0부터 n까지 반복
for j in range(min(i, k) + 1): # 리스트에 열로 사용할 j를 0부터 i까지 반복. 이때 i가 k보다 커지면 k까지만 반복
if j == 0 or j == i: # j가 0이거나 행과 열이 같으면 1을 저장
B[i][j] = 1
else: # 그렇지 않을 경우 위의 값과 왼쪽 값을 더해서 저장한다.
B[i][j] = B[i-1][j-1] + B[i-1][j]
return B[n][k]
반응형
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| [백준] 2217. 로프 (0) | 2020.05.09 |
|---|---|
| [백준] 11399. ATM (0) | 2020.05.09 |
| 동적계획법 소개 (0) | 2020.05.01 |
| [codeup] 3720. nCr (0) | 2020.04.20 |
| [codeup] 3014. 정렬을 빠르게 (0) | 2020.04.19 |
