https://codeup.kr/problem.php?id=3720
nCr (Hell)
첫째 줄에 n, r이 주어진다. ( 0 <= r <= n <= 1,000,000,000 )
codeup.kr
굉장히 쉬워보이는 문제이다.
nCr = n! / (r! * (n - r)!) 또는 C(n, r) = C(n-1, r) + C(n-1, r-1)
둘 중 하나를 이용하면 쉽게 풀릴 것처럼 보이는 문제이다.


그러나, 1차원적인 접근방법은 절대로 풀 수 없도록 하는 어마무시한 input data size이다.
1. 문제
nCr을 1999로 나눈 나머지를 구하라.
2. 알고리즘
뤼카의 정리를 이용한다.
https://ko.wikipedia.org/wiki/%EB%A4%BC%EC%B9%B4%EC%9D%98_%EC%A0%95%EB%A6%AC
뤼카의 정리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 뤼카의 정리(Lucas' theorem, -定理)는 수론과 조합론에서 이용되는 정리로, 프랑스인 수학자 에두아르 뤼카(Édouard Lucas)의 이름이 붙어 있다. 이 정리는 어떤 조합의 수를 소수 p에 대해 법 p 상에서 구할 때 간편한 계산 방식을 제공한다. 에두아르 뤼카가 처음 이 정리를 발표한 것은 1878년 논문에서였다.[1] 임의의 음이 아닌 정수 m과 n, 소수 p에 대하여 뤼카의 정리는 다음과 같이 합동식
ko.wikipedia.org
3. 주의할 점
C(n, r)을 구할 경우 시간복잡도는 O(nr)이다. 그러나 n과 r이 조금만 커져도 엄청나게 커진다.
예를 들어, n = 100, r = 50인 경우를 보자.
C(100, 50) = 100891344545564193334812497256 하물며, 데이터 입력값의 최대값인 10억이 들어온다면 무조건 메모리 초과 혹은 시간초과가 날 수 밖에 없다. 따라서 다른 접근법을 생각해야한다.
nCr문제는 일반적으로 어떤 수로 나눈 나머지를 구하는 경우가 많다. 여기서는 1999로 나눈 나머지를 구하는 것이 문제의 핵심이다. 이것은 다음과 같은 점화식으로 나타낼 수 있다.
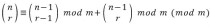
이 방법은 해결이 될까. n=1000000000, r=500000000인 경우 5 * 10^17이다. 컴퓨터의 초당 처리 속도가 약 4억번인 것을 감안하면 위 값을 구하는데 40년이라는 세월이 걸린다. 제출하고 40년뒤에 찾아와서 확인하면되나.
하지만 여기에 m이 소수라는 조건이 추가되면 뤼카의 정리를 이용할 수 있다.


이 공식을 이용하면 nCr mod p를 구하는데 시간복잡도가 O(p^2)으로 줄어든다.
예시>

위의 식을 뤼카의 정리를 이용해서 구해보자.
먼저 다음과 같이 1432와 342을 7진법 전개식으로 나타내야 한다.

따라서 다음과 같이 나타낼 수 있습니다.

이때

이면

으로 취급한다.
따라서

의 값이 0이라는 것을 알 수 있다.
4. 소스코드
n, r = map(int ,input().split())
p = 1999
def c(N, R):
global p
f = [1 for _ in range(p)]
for i in range(1, p):
f[i] = (f[i - 1] * i) % p
res = 1
while N and R:
n, r = N % p, R % p
if n < r:
res = 0
break
res = (res * f[n]) % p
for i in range(p-2):
res = ((res * f[r]) % p * f[n-r]) % p
N //= p
R //= p
return res
print(c(n, r))
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| DP. 동전 거스름돈과 이항계수 (0) | 2020.05.01 |
|---|---|
| 동적계획법 소개 (0) | 2020.05.01 |
| [codeup] 3014. 정렬을 빠르게 (0) | 2020.04.19 |
| [codeup] 3019. 스케줄 정리 (0) | 2020.04.19 |
| [codeup] 3004. 데이터 재정렬 (0) | 2020.04.19 |
