반응형
1. n-Queens 문제
n x n 체스판에서 n개의 퀸들을 서로 위협하지 않도록 배치하는 문제
2. 백트래킹
- 초기 상태에서 목표 상태로 가는 경로를 탐색하는 기법
- 해를 찾는 도중 해가 아니면 되돌아가서 다시 해를 찾는 기법
- 최적화(optimize)문제와 결정(decision)문제를 해결할 수 있다.
- 최적화 문제
- 미로 찾기, Subset sum 등
- 결정 문제
- n-Queen, Map coloring 등

루트까지 되돌아갔는데 더이상 선택지가 없다면 답이 없는 것이다.
백트래킹의 핵심은 상태 공간 트리를 탐색하는 것!
- 해를 찾기 위한 선택의 과정을 트리로 표현
- 트리의 내부 노드는 해로 가는 중간 상태
- 트리의 단말 노드는 하나의 후보해에 대한 최종 상태
- 상태 공간 트리를 깊이 우선 탐색(DFS)하는 방법이 백트래킹의 기본 알고리즘
3. 백트래킹 vs DFS
백트래킹은 탐색 중간에 해가 아니면 되돌아가는 가지치기(prunning)을 수행하므로 DFS에 비해 경우의 수가 줄어든다.
4. 8-Queens 문제
- 후보해 수 = C(64, 8) = 4426165368
- 실제 해의 수는 92개
- 약 44억 개의 후보해 중 실제 해 92개를 어떻게 최대한 효율적으로 찾아내는가
5. 4-Queens 문제
- 퀸들은 같은 행에 위치할 수 없다.
- 모든 경우의 수 = 4 * 4 * 4 * 4 = 256
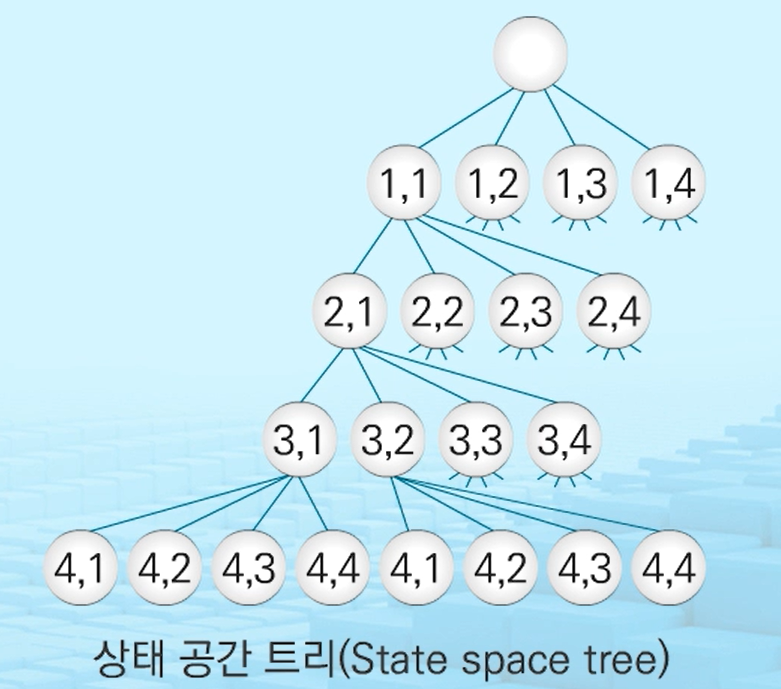
루트 높이를 0이라 할 때,
- 높이가 1인 노드 -> 첫번째 퀸의 위치가 선택된 상태
- 높이가 2인 노드 -> 두번째 퀸의 위치가 선택된 상태
백트래킹은 모든 후보해를 검사하지 않는다!
- 노드를 검사하여 유망하지 않으면 해당 노드의 부모로 되돌아가고(backtracking) 다음 자식노드로 간다.
- => 가지치기(prunning)
상태공간트리 DFS => 방문 노드 유망성 검사 => No 유망? => 부모노드로 backtracking
소스코드
일반적인 백트래킹 알고리즘
# v : node
def checknode(v) :
if promising(v): # v노드의 유망성 검사
if there is a solution at v: # 단말 노드 o => 해이면 해출력
write the solution
else:
for u in each child of v: # 단말노드 x => 자식노드에 대해 재귀호출
checknode(u)
# 유망하지않을 경우
# 재귀호출 하지않고 종료

반응형
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| Algorithm. 백트래킹 - 순열 (0) | 2020.05.22 |
|---|---|
| Algorithm. 백트래킹 - 부분집합 (0) | 2020.05.22 |
| 부분집합 bitwise 표현 (0) | 2020.05.18 |
| Algorithm. 2주차 스터디 계획 (0) | 2020.05.17 |
| Algorithm. 1주차 스터디 정리 (0) | 2020.05.17 |
