1. 탐욕(그리디) 알고리즘
- 최적화 문제를 해결하는 알고리즘
- 최적해를 구하는 근시안적인 방법
- 최적화 문제는 최적값(최대값 또는 최소값 등)을 구하는 문제
여러 경우 중 하나 선택 -> 선택시 마다 최적을 선택 -> 최종 해답 도달
- 대부분의 그리디 알고리즘은 단순하며, 제한적인 문제들에 적용
- 각 선택은 지역적으로 최적
- 지역적 최적해를 수집하여 최종 해답을 만들었다고해서 그것도 최적이라는 보장은 없다.
2. 수행 과정
- 해 선택
- 현재 상태에서 최적이라고 여겨지는 해답을 해집합에 추가
- 하나의 해 선택이 이루어지면 새로운 부분 문제 발생
- 실행 가능성 검사 실시
- 새로운 부분 해 집합의 실행가능 여부 확인
- 문제의 제약 조건 위반을 검사
- 해 검사
- 새로운 부분 해 집합이 문제의 해가 되는지 확인
- 전체 문제의 해가 완성되지 않았다면 해 선택부터 다시 시작
3. 동전 거스름돈 문제
거스름돈의 지폐와 동전 개수 최소화하기
1. 해 선택
> 가장 큰 단위 선택
2. 실행가능성 검사
> 액수가 거스름돈 초과하는지 확인
> 초과할 경우 한 단계 작은 단위 선택
3. 해 검사
> 액수 = 거스름돈
> 모자라면 해 선택으로 다시 시작
https://www.acmicpc.net/problem/5585
5585번: 거스름돈
문제 타로는 자주 JOI잡화점에서 물건을 산다. JOI잡화점에는 잔돈으로 500엔, 100엔, 50엔, 10엔, 5엔, 1엔이 충분히 있고, 언제나 거스름돈 개수가 가장 적게 잔돈을 준다. 타로가 JOI잡화점에서 물건�
www.acmicpc.net
4. 배낭 문제
배낭의 총 무게를 넘지 않으면서 가치의 초합이 최대가 되는 물건 선택해야 한다.
- S : 물건들의 집합
- Wi : 물건 i의 무게
- Pi : 물건 i의 가치
- W : 배낭이 수용가능한 총 무게
문제정의

배낭 총 무게를 넘지않으면서 물건들의 가치의 총합이 최대가 되는 "물건들의 집합"의 부분 집합을 구하는 문제
0-1 Knapsack vs Fractional Knapsack
1. 0-1 Knapsack
물건을 통째로 담아야한다.
2. Fractional Knapsack
물건을 쪼갤 수 있으며 가치 또한 (가치/나눈개수)로 줄어든다.
0-1 배낭문제
1. 완전검색
- 완전 검색으로 물건들의 집합 S에 대한 모든 부분집합 구함
- 부분 집합 중 배낭 총 무게 W를 초과하는 집합은 제외하고, 나머지에서 총 가치가 가장 큰 집합 선택
- 물건 개수 증가시 시간 복잡도 지수적으로 증가
- 원소 수 n인 집합의 부분집합 수 = 2^n
2. 그리디
W = 30 일때,
1) 값이 비싼 물건부터 채움
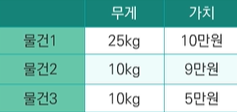
그리디 : 1 -> 10만원
최적해 : 2 + 3 -> 14만원
2) 무게가 가벼운 물건부터 채움

그리디 : 2 + 3 -> 14만원
최적해 : 1 -> 15만원
3) 무게 당 가치가 높은 순서로 채움

그리디 : 1 + 3 -> 190만원
최적해 : 2 + 3 -> 200만원
세 방법 모두 최적해를 구할 수 없다. 따라서 0-1 배낭문제는 그리디로 최적해를 구할 수 없다.
단, fractional knapsack문제는 그리디로 풀 수 있다.
W = 30 일때,
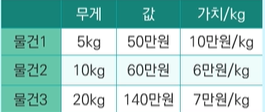
그리디 : 1 + 3 + 2의절반 -> 220만원
5. 활동 선택 문제 - 회의실 배정 문제
사용 가능한 회의실은 하나만 존재하고, 다수의 회의가 신청된 상태이다. 회의는 시작 시간과 종료 시간이 존재한다. 회의시간이 겹치는 회의는 동시 개최가 불가능할 때, 최대한 많은 회의가 열리도록 회의를 배정하는 경우를 구하라.
문제 정의
시작시간과 종료시간이 있는 n개의 활동집합에서 서로 겹치지않는 최대 개수 활동 집합을 구하는 문제
- 양립 가능한 활동들의 크기가 최대가 되는 S0,n+1의 부분집합을 선택하는 문제
- 종료 시간 순으로 활동들 정렬
- S0, n+1은 a0의 종료시간부터 an+1의 시작시간 사이에 포함된 활동들
- a0는 종료시간이 0, an+1은 시작시간이 무한대인 가상의 활동
문제 접근
- Si,j에서 종료시간이 가장 빠른 활동 am을 선택
- Si,m은 공집합이므로, am을 선택하면 공집합이 아닌 하위문제 Sm,j가 남는다.

그리디 적용
- S0,11에 대해서 a1 선택 -> S1,11 풀이 : S1,11 = {a4, a6, a7, a8, a10}
- S1,11에 대해서 a4 선택 -> S4,11 풀이 : S4,11 = {a8, a10}
- S4,11에 대해서 a8 선택 -> S8,11 풀이 : S8,11 = {a10}
- S8,11에 대해서 a10 선택
종료시간이 가장 빠른 회의를 선택하는 것은 탐욕적 선택으로 지역적으로 최적해이다. 그리고 최적해를 보장한다. 하나의 선택을 수행 후 크기가 줄어든 하위 문제를 똑같이 풀면 된다.
슈도코드
# A : 정렬된 활동들의 집합
# S : 선택된 활동들의 집합
# si : 시작시간
# fi : 종료시간, 1 <= i <= n
S = {a1} # 첫번째 활동을 선택하고 해집합에 추가
i = 1
for j in range(2, n+1):
if fi <= sj:
S = S U {aj}
i = j재귀코드
# A : 정렬된 활동들의 집합
# S : 선택된 활동들의 집합
# si : 시작시간
# fi : 종료시간, 1 <= i <= n
Recursive_Selection(i, j):
m = i + 1
while m <= j and sm < fi: # 종료 시간이 가장 빠른 활동 선택
m = m + 1
if m <= j : return {am} U Recursive_Selection(m, j)
else : return {} # 공집합
6. 그리디가 최적해를 구하는 조건
1. 그리디 선택 속성
매 단계에서의 탐욕적 선택이 최적해로 갈 수 있다.
2. 최적 부분 구조
하나의 선택을 하면 하위 문제가 남는다.
원문제 최적해 = 탐욕적 선택 + 하위 문제 최적해
7. baby-gin
각 6개의 숫자를 카운트리스트에 저장하고 카운트 리스트의 각 원소를 체크하여 런과 트리플렛 체크를 통해 베이비진 여부를 판단한다.
8. 그리디 vs 동적계획법

9. 대표적인 그리디 알고리즘

'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| Algorithm. 1주차 스터디 정리 (0) | 2020.05.17 |
|---|---|
| Algorithm 03. 분할 정복 (0) | 2020.05.17 |
| [백준] 1969. DNA (0) | 2020.05.16 |
| Algorithm 01. 완전검색 2 (0) | 2020.05.15 |
| Algorithm 01. 완전 검색 1 (0) | 2020.05.14 |
